Classification: premier modèle avec les SVM

Pour illustrer le travail de données nécessaire pour construire un modèle de Machine Learning, mais aussi nécessaire pour l’exploration de données avant de faire une régression linéaire, nous allons partir du jeu de données de résultat des élections US 2016 au niveau des comtés

Exercise 1: importer les données

Importer les données (l’appeler df) des élections américaines et regarder les informations dont on dispose
Créer une variable republican_winner égale à red quand la variable rep16_frac est supérieure à dep16_frac (blue sinon)
Représenter une carte des résultats avec en rouge les comtés où les républicains ont gagné et en bleu ceux où se sont les démocrates

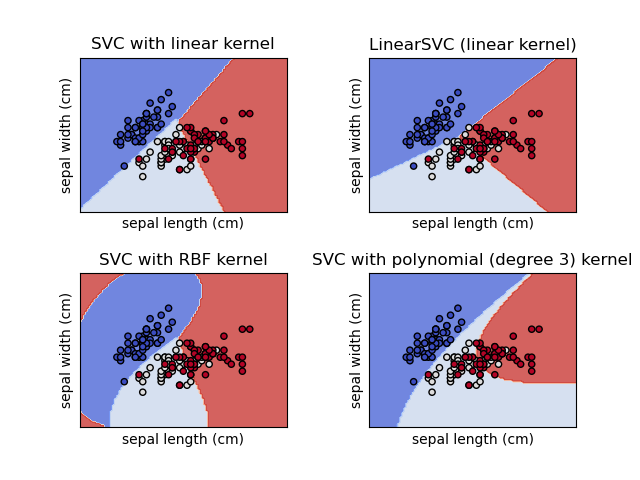
La méthode des SVM (Support Vector Machines)

L’une des méthodes de Machine Learning les plus utilisées en classification est les SVM. Il s’agit de trouver, dans un système de projection adéquat (noyau ou kernel), les paramètres de l’hyperplan (en fait d’un hyperplan à marges maximales) séparant les classes de données:

Formalisation mathématique

On peut, sans perdre de généralité, supposer que le problème consiste à supposer l’existence d’une loi de probabilité $P (x, y)$ ( $P \to - 1, 1$ ) qui est inconnue. Le problème de discrimination vise à construire un estimateur de la fonction de décision idéale qui minimise la probabilité d’erreur, autrement dit $θ = \arg min_{Θ} P (h_{θ} (X) \neq y | x)$

Les SVM les plus simples sont les SVM linéaires. Dans ce cas, on suppose qu’il existe un séparateur linéaire qui permet d’associer chaque classe à son signe:

$h_{θ} (x) = signe (f_{θ} (x)); avec f_{θ} (x) = θ^{T} x + b$ avec $θ \in R^{p}$ et $w \in R$ .

Lorsque des observations sont linéairement séparables, il existe une infinité de frontières de décision linéaire séparant les deux classes. Le “meilleur” choix est de prendre la marge maximale permettant de séparer les données. La distance entre les deux marges est $\frac{2}{| | θ | |}$ . Donc maximiser cette distance entre deux hyperplans revient à minimiser $| | θ | |^{2}$ sous la contrainte $y_{i} (θ^{T} x_{i} + b) \geq 1$ .

Dans le cas non linéairement séparable, la hinge loss $max (0, y_{i} (θ^{T} x_{i} + b))$ permet de linéariser la fonction de perte:

ce qui donne le programme d’optimisation suivant:

$\frac{1}{n} \sum_{i = 1}^{n} max (0, y_{i} (θ^{T} x_{i} + b)) + λ | | θ | |^{2}$

La généralisation au cas non linéaire implique d’introduire des noyaux transformant l’espace de coordonnées des observations.

Exercice

Premier algorithme de classification

Créer une variable dummy y dont la valeur vaut 1 quand les républicains l’emportent
Créer des échantillons de test (20% des observations) et d’estimation avec comme features: 'less_than_high_school', 'adult_obesity', 'median_earnings_2010_dollars' et comme label la variable y. Pour éviter le warning

A column-vector y was passed when a 1d array was expected. Please change the shape of y to (n_samples, ), for example using ravel()

à chaque fois que vous estimez votre modèle, vous pouvez utiliser DataFrame[['y']].values.ravel() plutôt que DataFrame[['y']] lorsque vous constituez vos échantillons.

Entraîner un classifieur SVM avec comme paramètre de régularisation C = 1. Regarder les mesures de performance suivante: accuracy, f1, recall et precision. Vérifier la matrice de confusion: vous devriez voir que malgré des scores en apparence pas si mauvais, il y a un problème
Refaire les questions précédentes avec des variables normalisées. Le résultat est-il différent ?
Changer de variables x. Prendre uniquement dem12_frac et median_earnings_2010_dollars. Regarder les résultats, notamment la matrice de confusion
Faire une 5-fold validation croisée pour déterminer le paramètre C idéal.

Le classifieur avec C = 1 devrait avoir les performances suivantes:

Métrique	Score
Accuracy	0.8025478
Recall	0.8025478
Precision	1
F1	0.8904594

## <sklearn.metrics._plot.confusion_matrix.ConfusionMatrixDisplay object at 0x0000000007C769A0>

Notre classifieur manque totalement les labels 0, qui sont minoritaires. Une raison possible ? L'échelle des variables: le revenu a une distribution qui peut écraser celle des autres variables, dans un modèle linéaire. Il faut donc, a minima, standardiser les variables. Néanmoins, ici cela n’apporte pas de gain:

## <sklearn.metrics._plot.confusion_matrix.ConfusionMatrixDisplay object at 0x0000000007C76F10>

Il faut donc aller plus loin : le problème ne vient pas de l'échelle mais du choix des variables. C’est pour cette raison que l'étape de sélection de variable est cruciale. En utilisant uniquement le résultat passé du vote démocrate et le revenu (dem12_frac et median_earnings_2010_dollars), on obtient un résultat beaucoup plus cohérent:

## <sklearn.metrics._plot.confusion_matrix.ConfusionMatrixDisplay object at 0x000000000A090550>

Métrique	Score
Accuracy	0.94061
Recall	0.9668616
Precision	0.9612403
F1	0.9640428

Last updated on 21 Oct 2020
Published on 15 Oct 2020
Edit on GitHub